从Training Dynamics到Outlier——LLM模型训练过程中的数值特性分析
Training Dynamics是一个未被严格定义的词,泛指模型训练过程中观测到的各种现象、变化和行为规律。我们可以从loss、泛化loss、梯度大小以及等等表现来观察模型内部的演变机制,并总结出类似涌现现象(Emergency)、Scaling Law、Double Decent和Gradient Pathologies等现象。
特别地,权重矩阵与激活值的动态演变(Dynamics)会直接影响数值表达范围,进而决定硬件计算精度选择与量化误差控制策略。本文聚焦Transformer架构中关键组件的数值动态特性,重点分析其对低精度训练与推理的工程影响。
权重与激活的数值演变特征
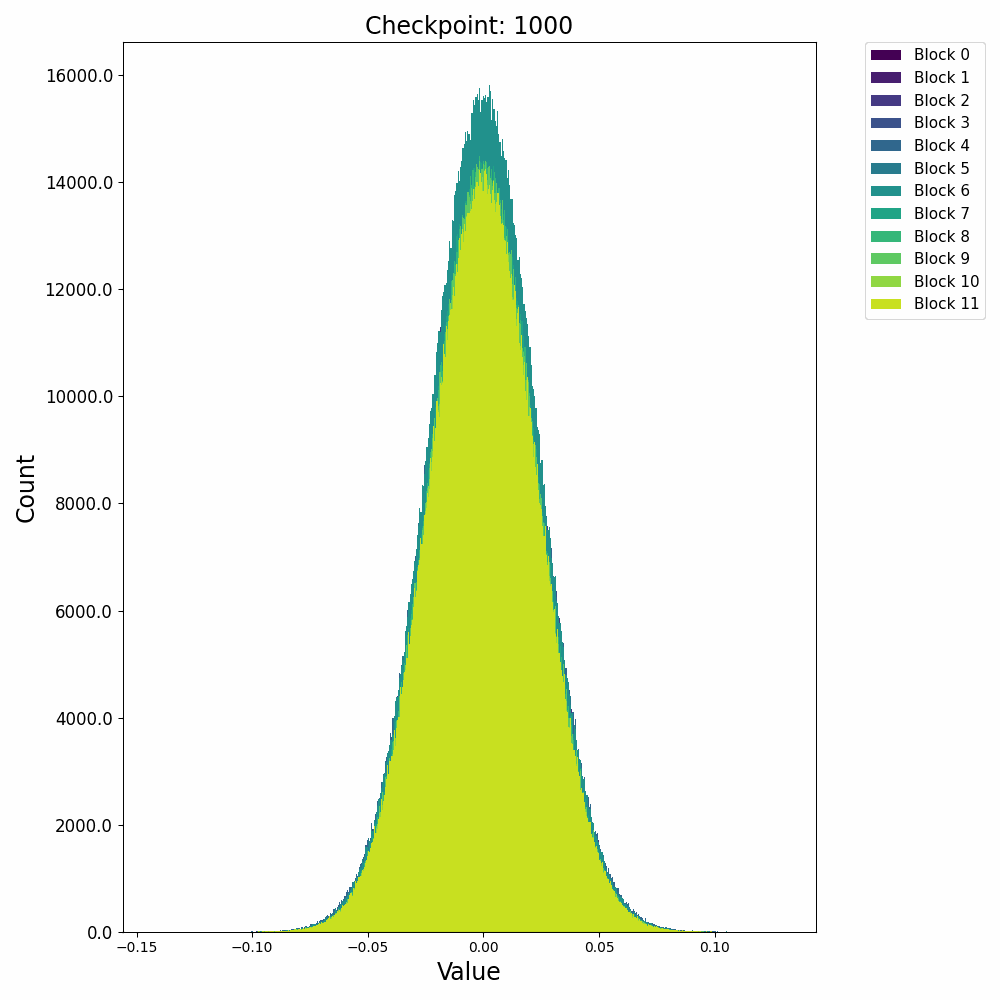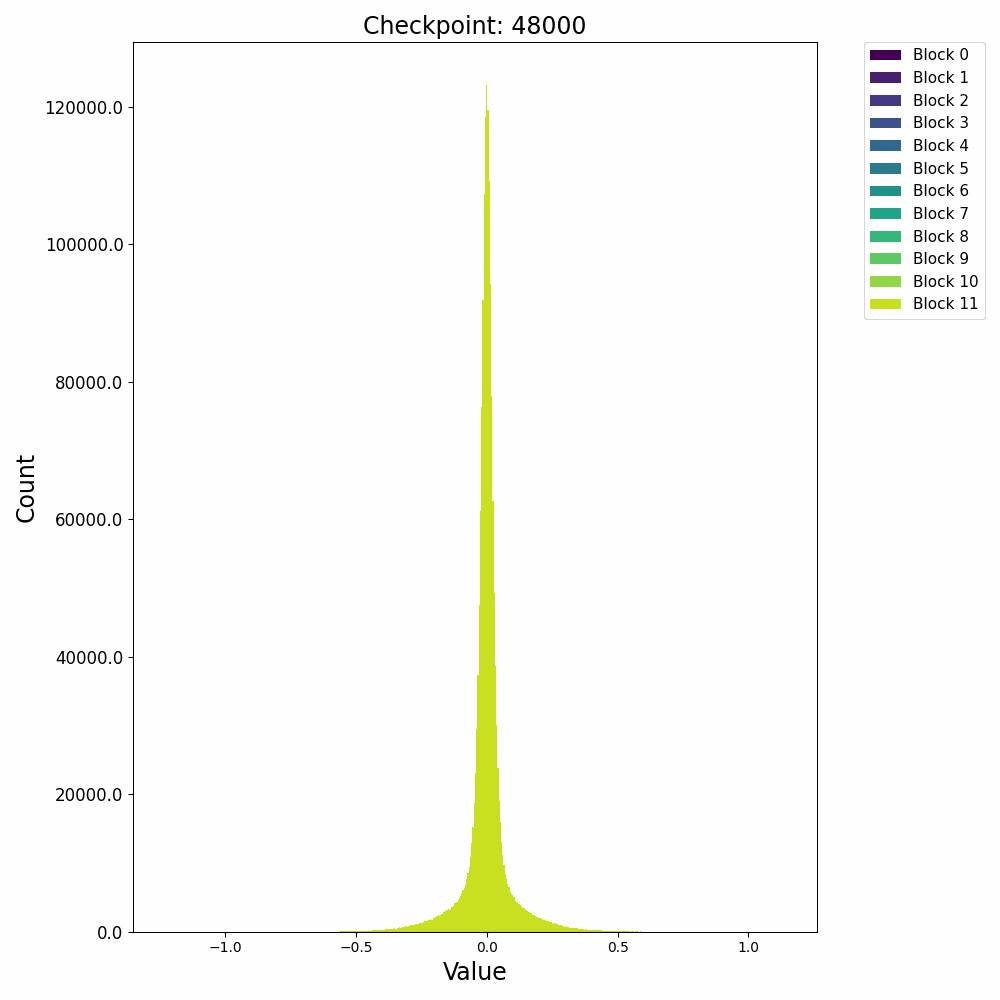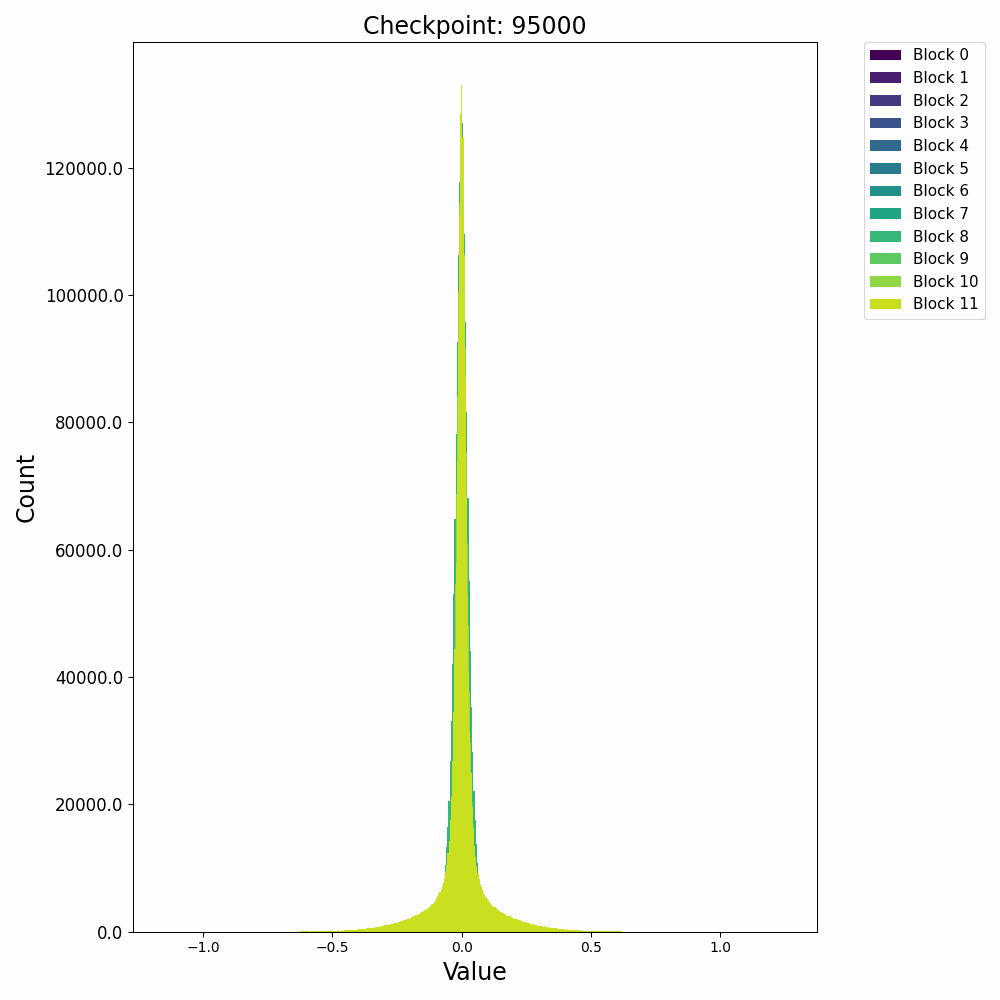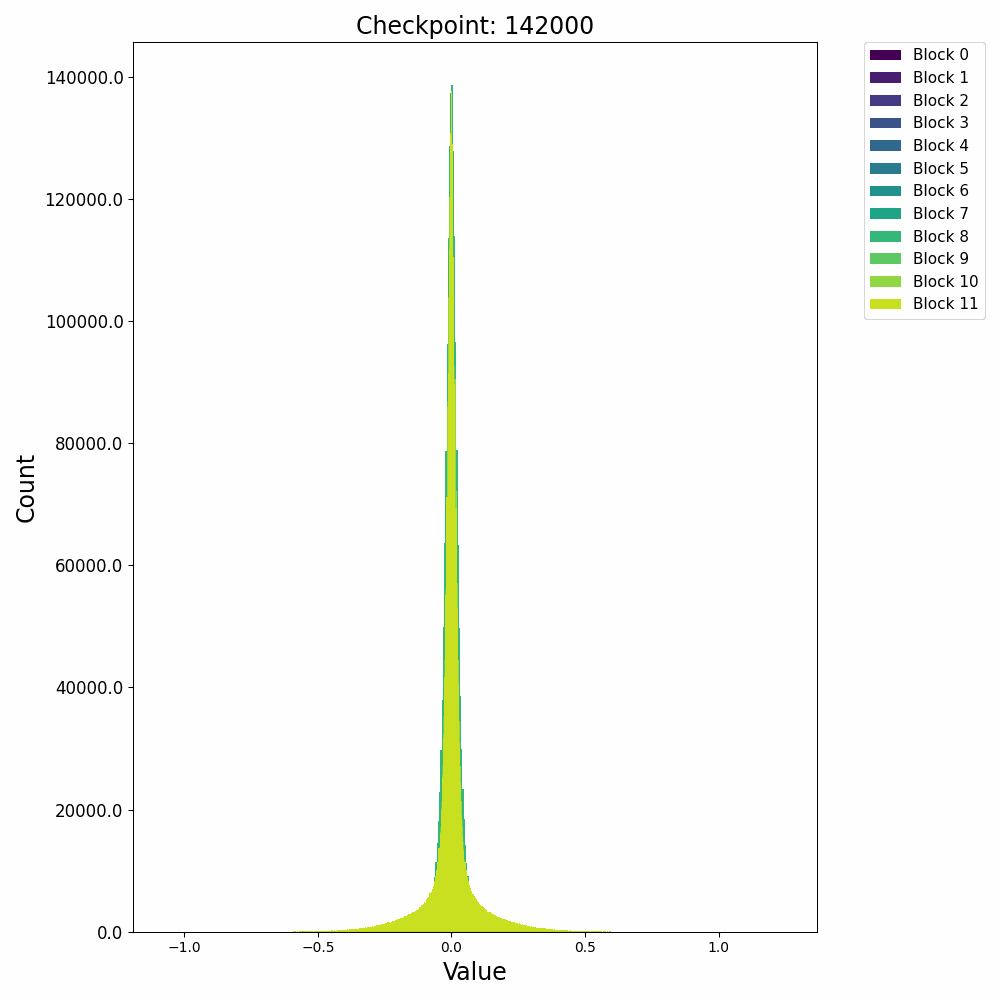
这里先给出权重与梯度的直观数值变化,帮助直观理解训练过程。下图取自某开源仓库1,展示了权重数值的直方分布随训练进行的变化情况:
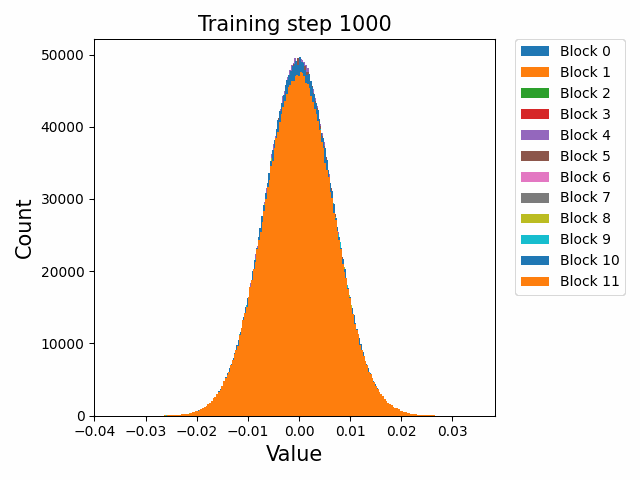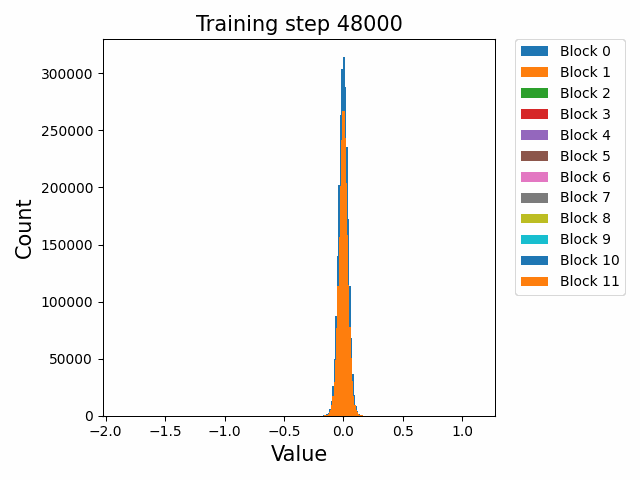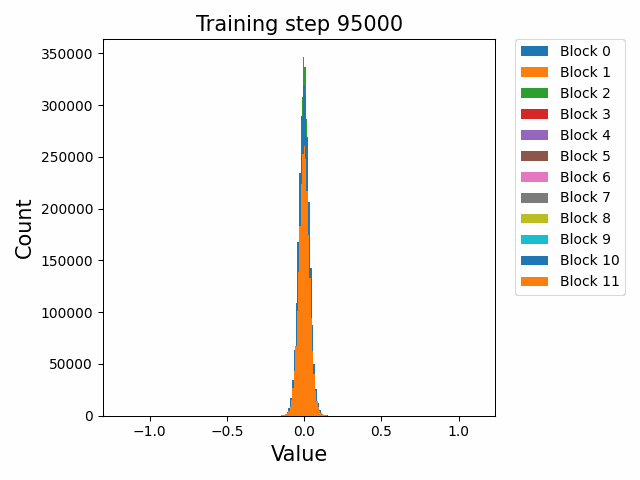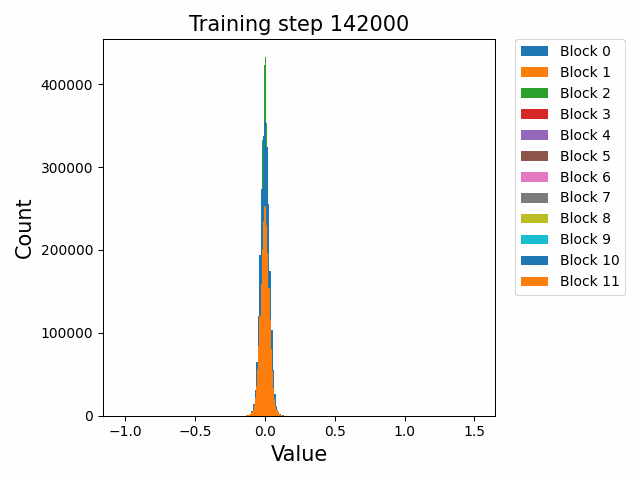
可以发现,各个block的FFN部分权重从随机初始化的高斯分布,开始时较为稳定;在2000 step左右开始剧烈变化;随后整体分布再次稳定下来。权重整体保留了高斯分布,但是存在一些不是非常大的outlier。
接下来再看一下激活值的分布变化,在训练开始后,残差激活值迅速从高斯分布转变为逻辑分布(Logistic Distribution),并且出现较大的outlier:
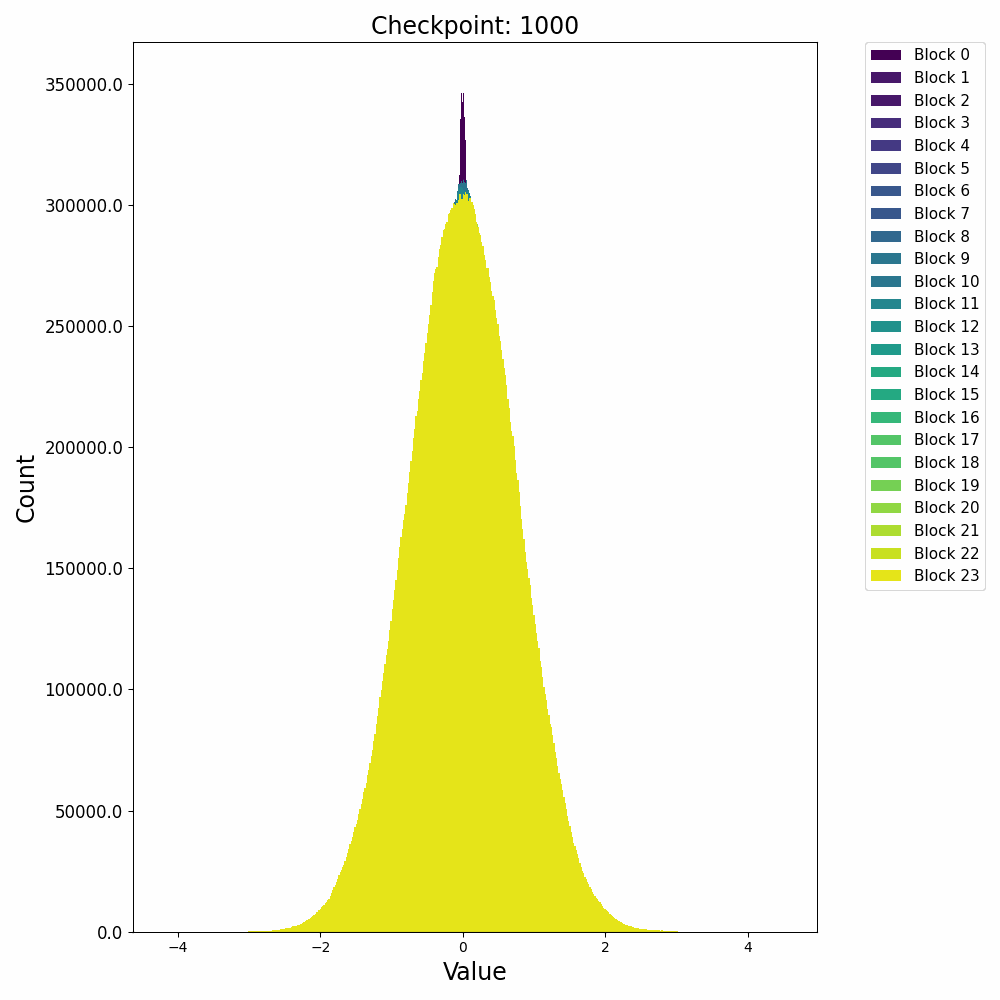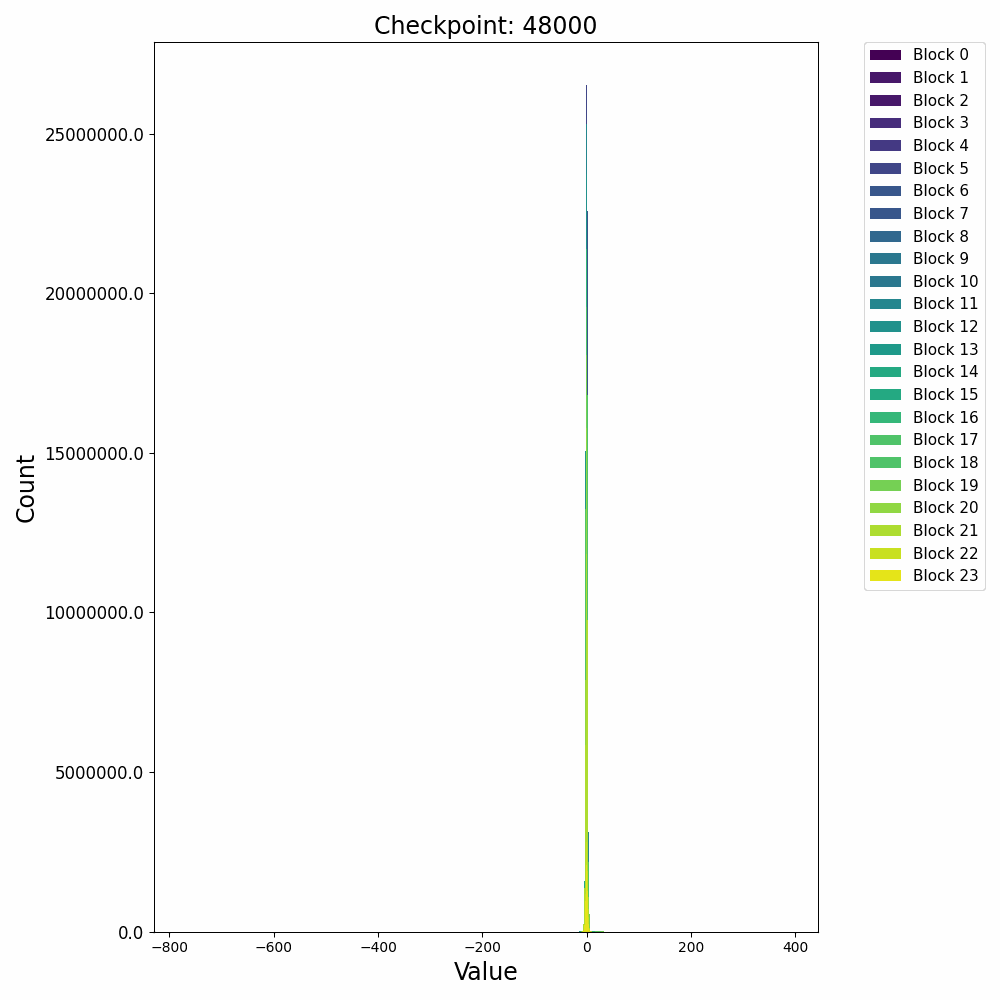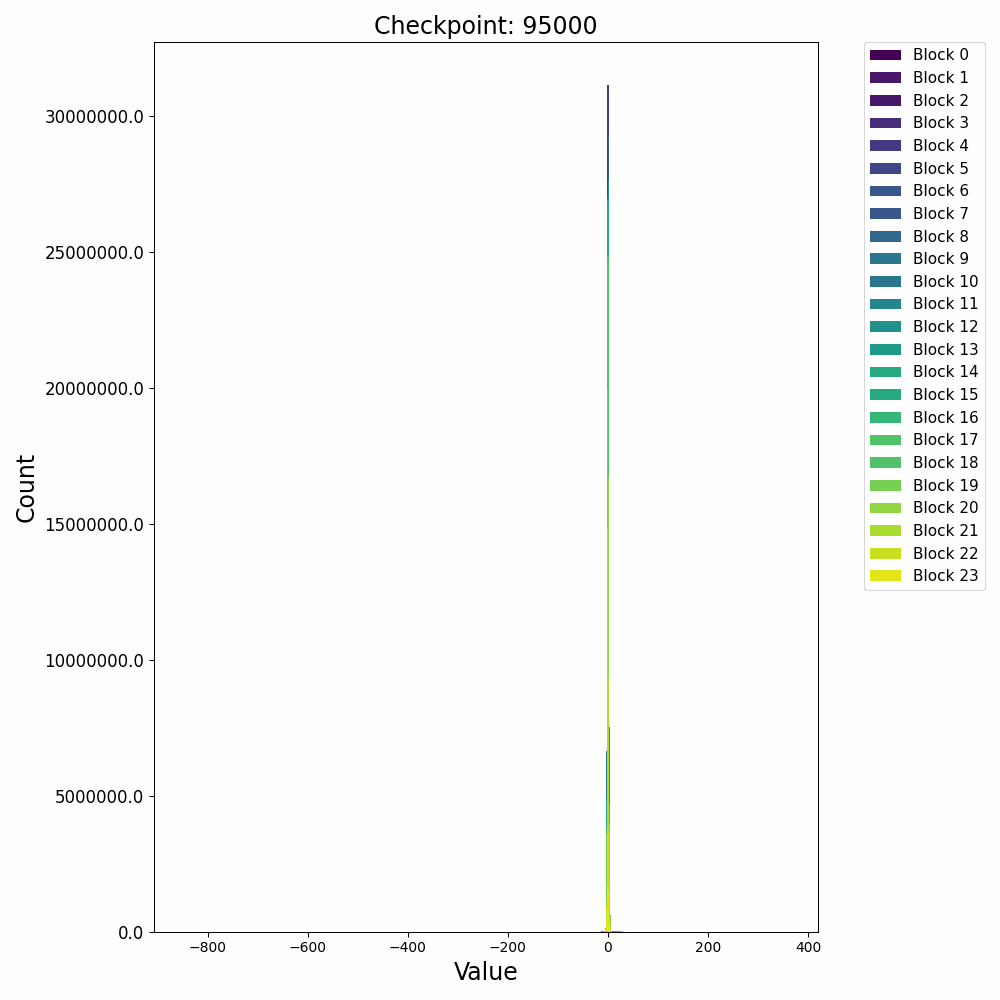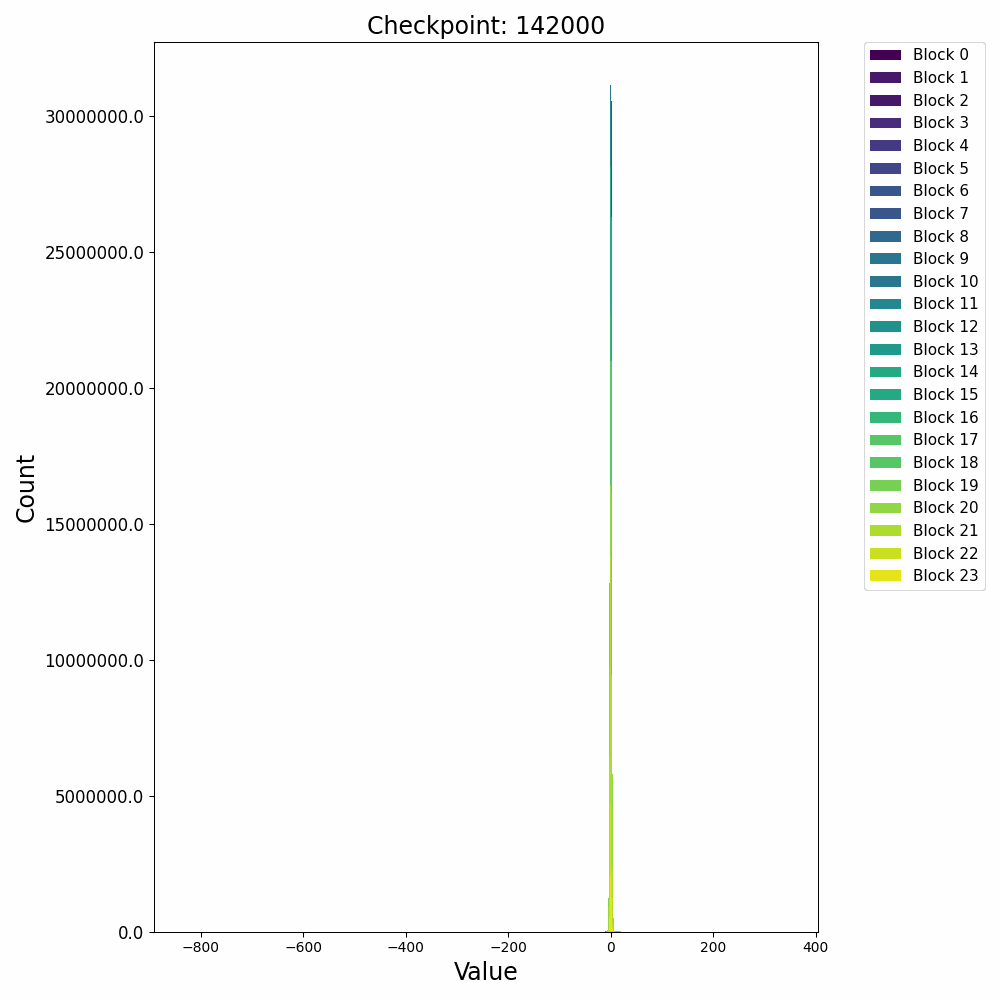
这种激活上的outlier会对模型量化过程产生极大的影响,因此诸如AWQ等量化方法会重点关注激活中的outlier情况,以保证模型推理时的精度。
梯度分布的变化趋势与权重类似,训练过程也未出现较大的outlier,说明梯度本身也具备较好的稳定性,存在低精度计算和存储的可能性。