INT8 也能训练

在前一篇博客中，我们深入探讨了 DeepSeek V3 如何通过 FP8 实现高效训练，并成功克服了精度挑战。本文探讨另一个问题：如果用 INT8 代替 FP8 做训练，会发生什么？

INT8 量化 ¶

给定一个浮点数向量 \(x \in \mathbb{R}^n\)，INT8 量化的目标是将其映射到 [-128, 127] 的整数空间。这一过程需要确定缩放因子 \(\alpha\) 和零点偏移 \(\beta\)，使得：

\[ x_q = round(\frac{x}{\alpha}) + \beta \]

其中 \(x_q\) 表示量化后的 INT8 值。缩放因子 \(\alpha\) 通常通过以下方式计算：

\[ \alpha = \frac{max(|x|)}{127} \]

这确保了量化后的值不会超出 INT8 的表示范围。而零点偏移 \(\beta\) 在对称量化场景下通常设置为 0，在非对称量化时则需要根据数据分布来确定。

对于 LLM 训练场景，由于权重和激活值通常呈现对称分布，我们可以使用对称量化方案：

def symmetric_quantize(x: torch.Tensor) -> Tuple[torch.Tensor, float]:
    alpha = x.abs().max() / 127.0  # 计算缩放因子
    x_q = torch.round(x / alpha)   # 量化
    x_q = torch.clamp(x_q, -128, 127)  # 截断
    return x_q, alpha

反量化操作则是将 INT8 值映射回浮点数空间：

\[ x_r = (x_q - \beta) \times \alpha \]

其中 \(x_r\) 是反量化后的浮点数值。在对称量化场景下，由于 \(\beta = 0\)，反量化简化为：

def symmetric_dequantize(x_q: torch.Tensor, alpha: float) -> torch.Tensor:
    return x_q * alpha

与 FP8 的浮点量化不同，INT8 采用均匀量化方案：

优势区间：大值区域精度更高（固定量化步长）
劣势区间：小值区域精度较低（相对误差更大）

这种特性使得 INT8 对数据分布形态更为敏感，需要针对性优化策略。

INT8 量化误差分析 ¶

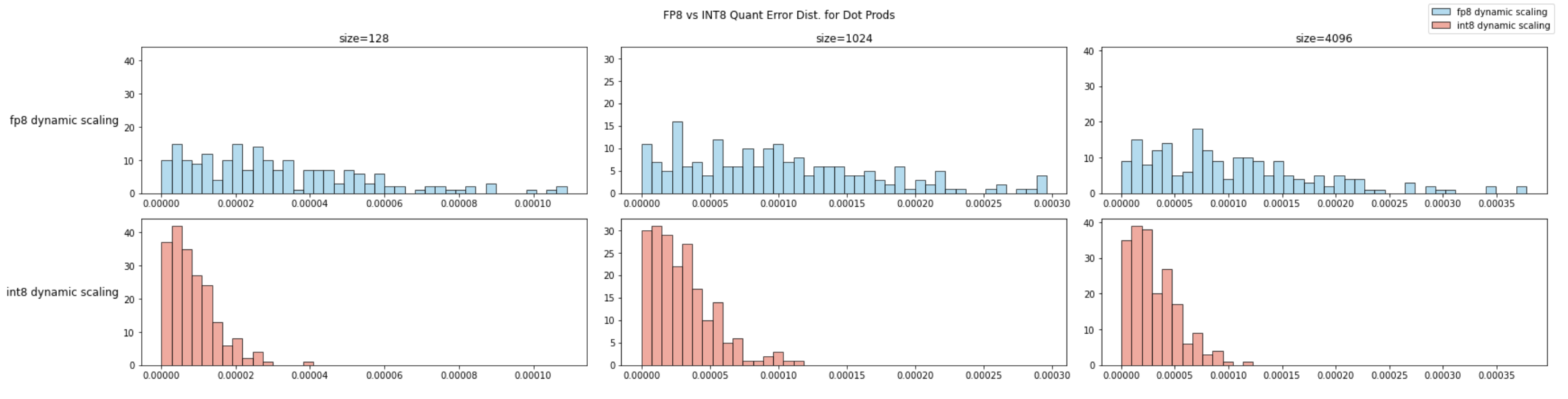
针对 3 种不同的向量长度（128/1024/4096）分别进行 200 次向量内积实验，并分别计算 FP8 与 INT8 量化噪声分布：

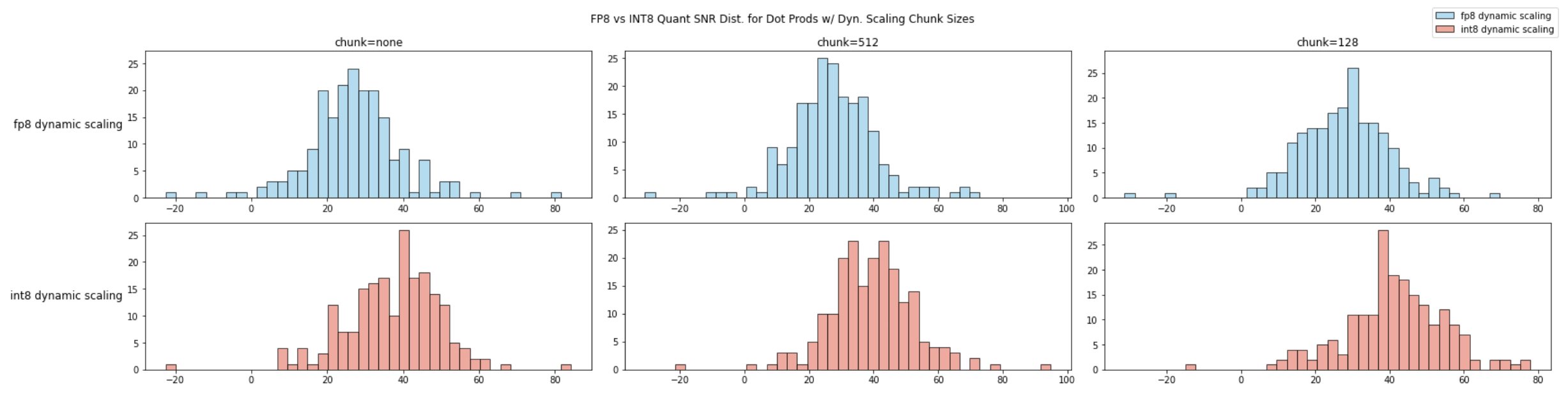
从定性分析来看，INT8 的绝对误差的分布更加集中在零附近，且最差情况也优于 FP8。我们进一步引入分块量化，看 INT8 量化方法的上限如何：

我们比较向量长度为 4096 情况下，使用分块动态 scaling 与高精度累加策略时 FP8 与 INT8 向量内积的信噪比。相同的 chunksize 下，INT8 的信噪比略优于 FP8。

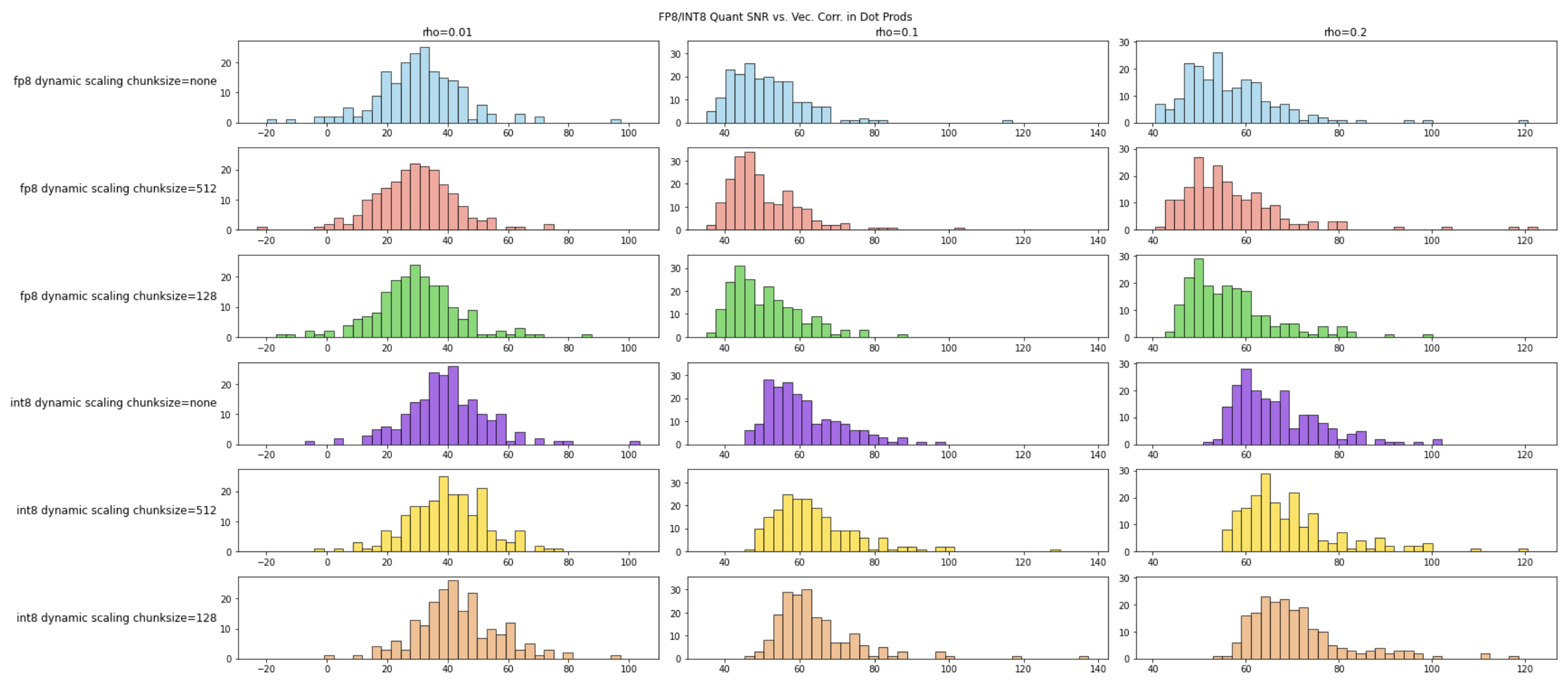
最后，我们对比下向量相关性对量化噪声的影响。实验使用长度为 4096 的向量，对比在 \(\rho \in [0.01, 0.1, 0.2]\) 三种情况下的信噪比：

实验发现，在相同相关性条件下，分块量化的 INT8 内积信噪比优于 FP8，且分块大小为 512 的 INT8 信噪比优于分块大小 128 的 FP8。具体实验代码见：https://github.com/reiase/ieee754_simulation/blob/master/simfloat_fp8_vs_int8.ipynb

一些讨论 ¶

通过信噪比的实验，我们发现使用分块量化的 INT8 向量内积精度并不逊于 FP8，信噪比分布甚至优于相同配置的 FP8。实验过程中也发现量化时的舍入策略对信噪比影响巨大，必须严格使用四舍五入的舍入策略才能保证 INT8 的精度。单纯从信噪比来看，如果仅仅像 TransformerEngine 那样替代 LLM 中原有的矩阵乘法，分块量化的 INT8 应该不会有太大问题。推理阶段也可以使用类似 LLM.int8 的方法¹来保证精度。

FP8 E4M3 的最大值为 448，而 INT8 的最大值为 127。动态范围上 FP8 E4M3 并没有太多优势。DeepSeek 的 FP8 方案的成功证明了 E5M2 这个高动态范围格式比较鸡肋，徒增复杂度。另一方面也启发了对 E4M3 格式的进一步探索：是否可以进一步舍弃 E4M3 的指数量化，而该用 INT8 的均匀量化。

LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale ↩