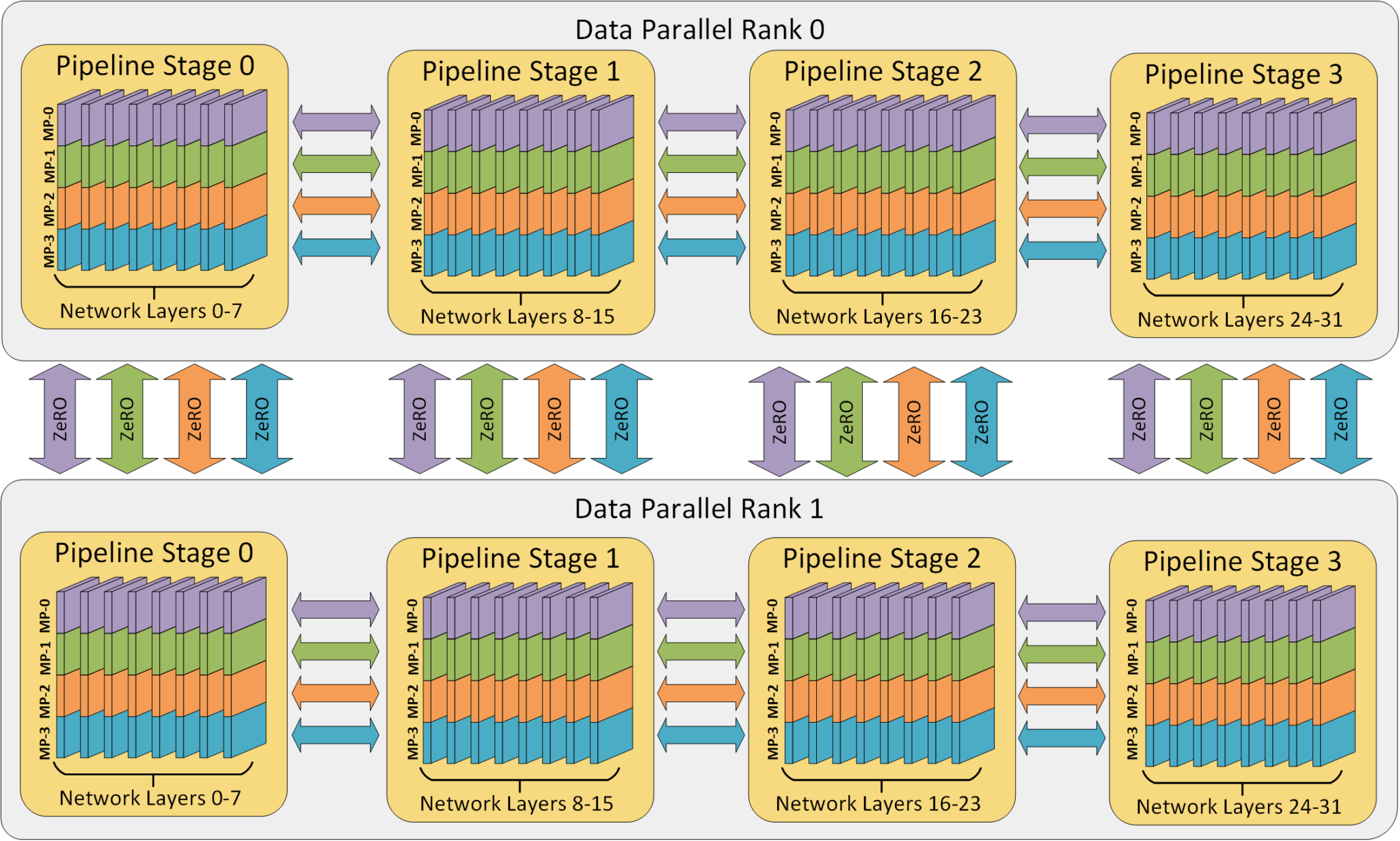
关于分布式模型并行的分正式评论
关于Data Parallel(DP)、Tensor Parallel(TP)和Pipeline Parallel(PP)等分布式并行策略,与Megatron、DeepSpeed和FSDP等实现的一些深入研究与讨论。分布式并行训练主要解决两类问题:
- 模型分片:模型大小远超单节点存储上来,需要多节点分片存储和计算担;
- 并行训练:提高单位时间内的算力密度,进而降低整体训练时间;
分布式并行训练几乎总是会引入昂贵的成本,比如增加了昂贵的多节点通信、引入了额外的多机稳定性问题、以及额外的开发与调试成本等,因此我们应该尽量避免引入分布式并行训练。而不得不引入分布式训练的场景中,也应充分考虑通信开销,尽量降低并行的规模。
3D模型并行¶
根据切分维度的不同,并行策略主要分为如下几类:
- Data Parallel(DP):将数据切分成N份,每个instance采用完全相同的配置,在计算梯度后通过all reduce全局同步梯度,并分别更新;
- Tensor Parallel(TP):将每个tensor切分成N份,在矩阵乘法等计算时进行同步;也称为横切
- Pipeline Parallel (PP):将模型按执行前后顺序切分多分(通常按layer切分),并根据顺序依次执行;
- Zero Redundancy Optimizer(ZeRO):同样将tensor切分成N份,但是在前向与后向计算时在每个分布式节点重建原始Tensor;
- Sequence Parallel(SP):在超长序列上进行训练时,将计算切分至多个节点;
Data Parallel¶
Data 并行一般是指根据计算资源将模型复制多个副本,每个模型副本独立进行数据加载与前后项计算,之后通过一个all reduce通信来同步梯度,最后再分别更新权重。
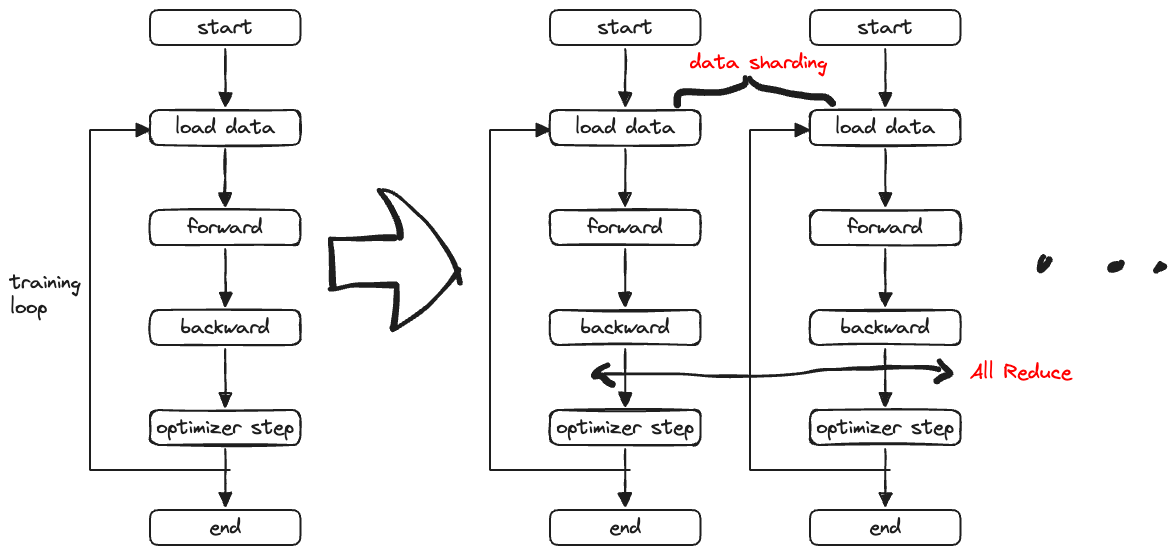
从单节点训练到多节点只需要改动两个地方:
- data loader根据对训练数据切片,并只读取对应分片的数据;
- backward之后通过all reduce同步梯度;
在PyTorch中两者分别通过torch.utils.data.distributed.DistributedSampler与torch.nn.parallel.DistributedDataParallel实现。
ZeRO: Zero Redundancy Optimizer¶
通过Data Parallel比较容易实现加速训练,但对于一些参数规模较大的模型,单节点的内存/显存难以放下,此时就无法通过简单的Data Parallel的数据切片来实现加速了。ZeRO技术主要尝试通过对模型状态切片,实现大模型的Data Parallel训练。具体原理如下图所示:
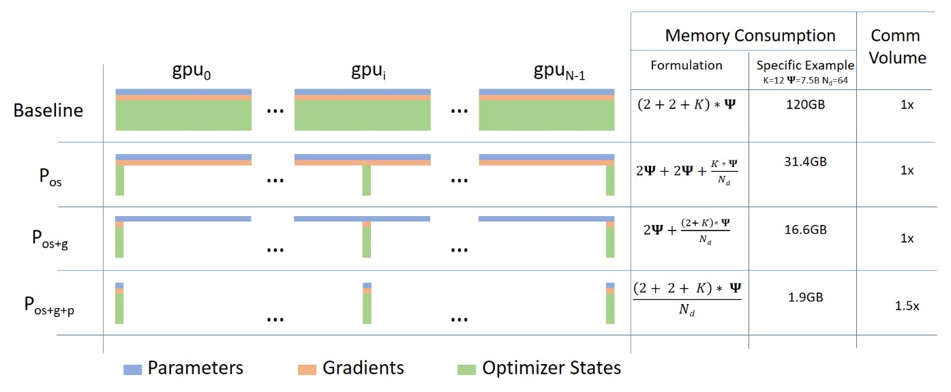
训练过程中模型状态可分为三部分:参数(Parameters)、 梯度(Gradients)和优化器状态(Optimizer States),我们可以将三者分别进行切分并存储到多个节点上去。根据切分方式的不同可以分为三个stage:
- ZeRO Stage 1:切分Optimizer States
- ZeRO Stage 2:切分Optimizer States与Gradients
- ZeRO Stage 3:切分Parameters
其中ZeRO1和ZeRO2并不会增加通信量,因此实际工程中被采用更多。
FSDP: Fully Sharded Data Parallel¶
FSDP是PyTorch在v1.11之后引入的内置Data Parallel并行模式。PyTorch官方在Data Parallel技术的发展路径是DP -> DDP -> FSDP,不断吸纳来自开源社区的新技术。
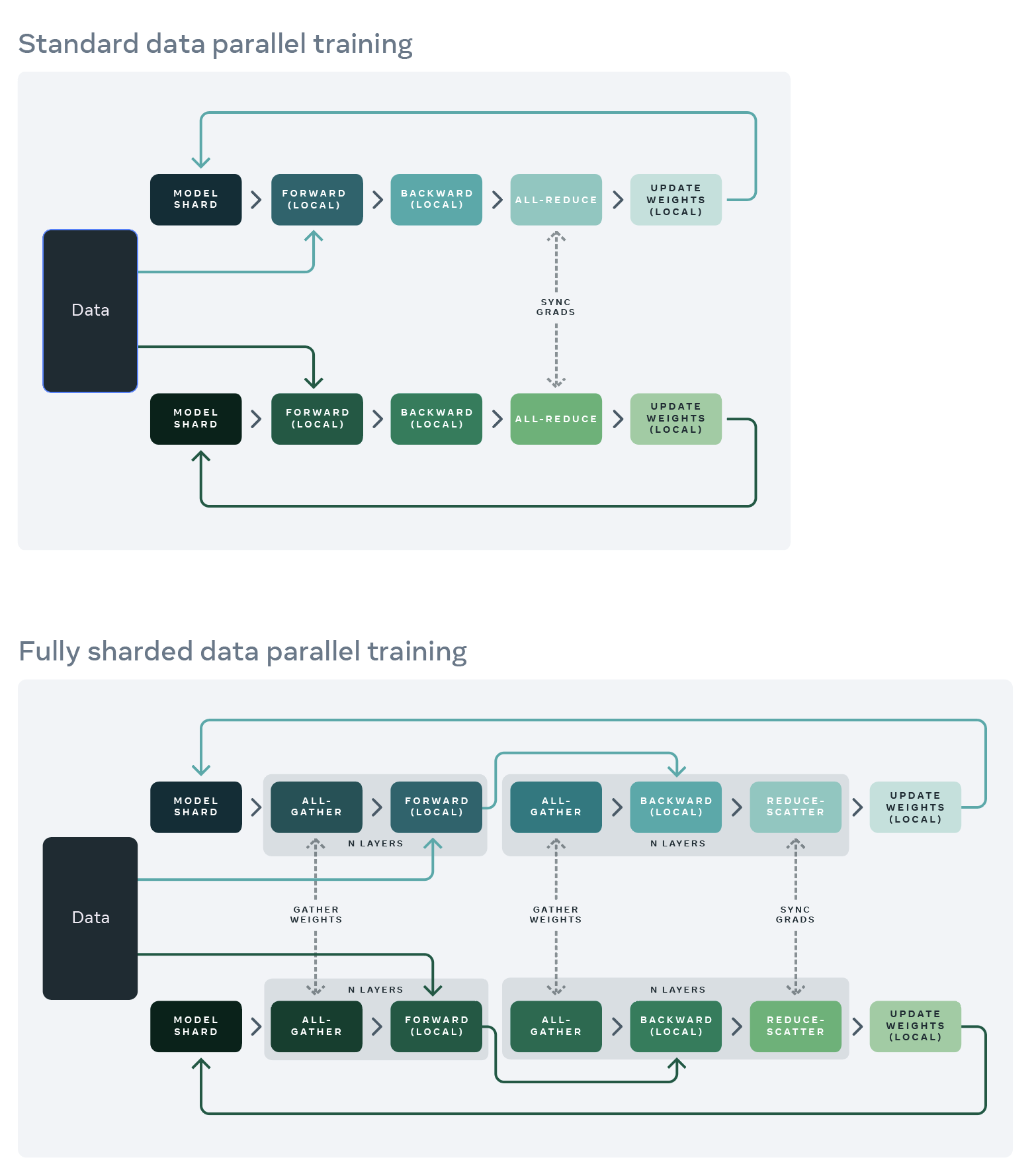
Tensor Paralle¶
对于一些语言模型来说,权重、梯度以及优化器状态可能并不是内存/显存占用的大头,激活值同样会占用大量内存。因此仅仅使用ZeRO技术并不能很好支持超大规模语言模型。此时需要Tensor Parallel进一步对激活值进行切分。
Tensor Parallel技术的基础是矩阵分块乘法,如下图所示:
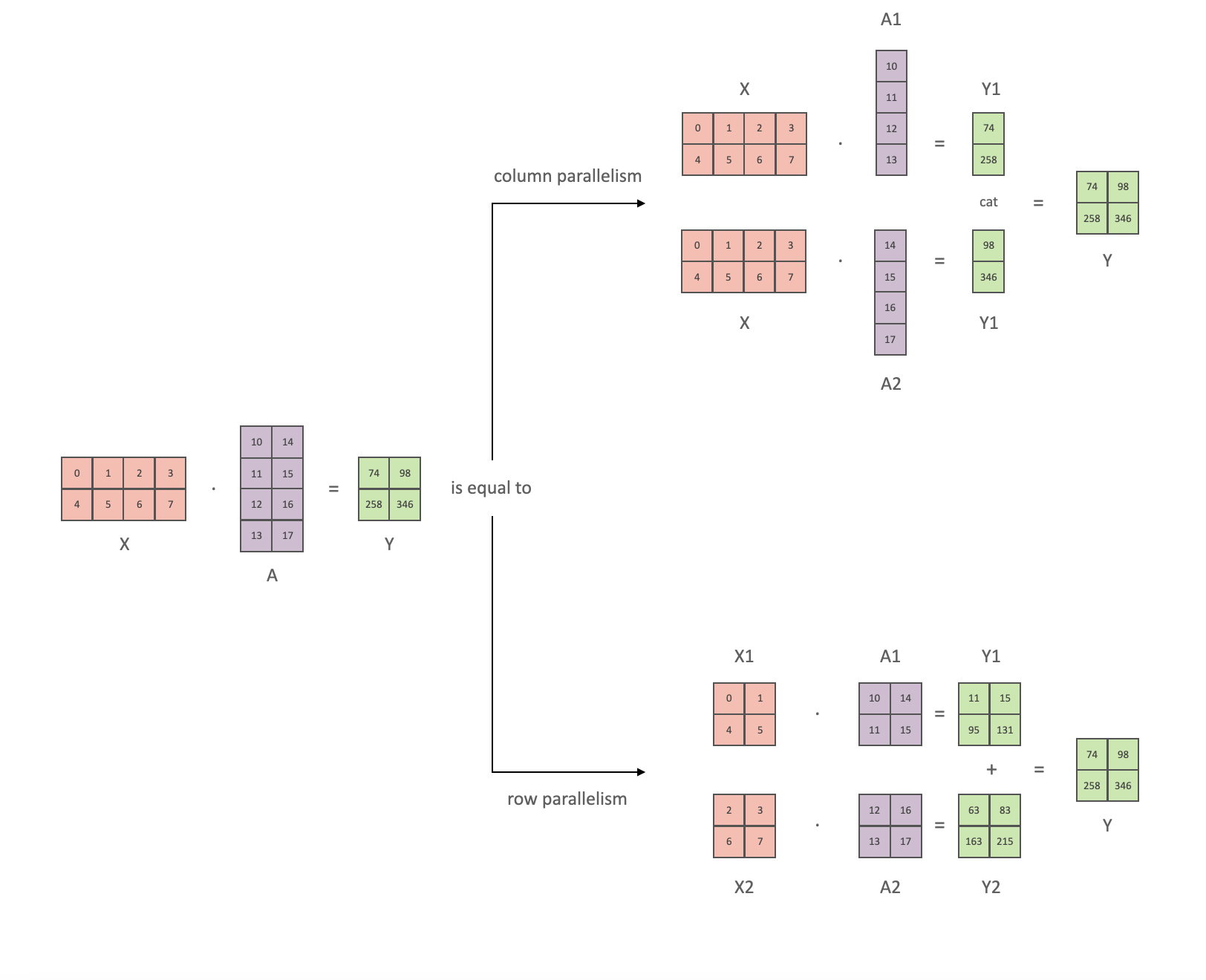
矩阵乘法的并行可分为列并行与行并行:
- 列并行:
$$
GeLU(WA) = GeLU(W[A_1, A_2, …, A_n]) = [GeLU(WA_1),GeLU(WA_2),…,GeLU(WA_n)]
$$
- 行并行:$$
GeLU(WA) = GeLU(
[W_1, W_2, …, W_n]
\left [
\begin{smallmatrix}
A_1 \
A_2 \
… \
A_n
\end{smallmatrix}
\right ]
) = GeLU(W_1A_1+W_2A_2+…+W_nA_n)
$$