关于Scaling Law的非正式评论
大模型被广泛关注的起点是OpenAI发布ChatGPT,凭借优秀的对话能力与In-Context Learning的能力,吸引了整个AI圈的关注。
LLM技术的发展主要得益于Scaling Law给出的一系列预测,这些预测主导了最近几年LLM模型在参数、数据和算力规模上快速增长。
甚至有人提出了”Scale is All You Need!”。本文主要讨论LLM行为的可预测性,记录关于Scaling Law、Grokking和Double descent等empirical phenomenon的讨论。
大模型的良好泛化性¶
OpenAI在GPT3论文中提出GPT-3等语言模型(language model)是few shot learner。这一概念出自In-Context Learning,具体是指在模型预测时通过上下文中给出足够的背景知识和任务描述,然后直接预测1,比如:
- Zero-shot(没有示例):{8+9=?}
- One-shot(一个示例):5+5=10, {8+9=?}
- Few-shot(多个示例):6+7=13,6+6=12,5+5=10, {==8+9=? ==}
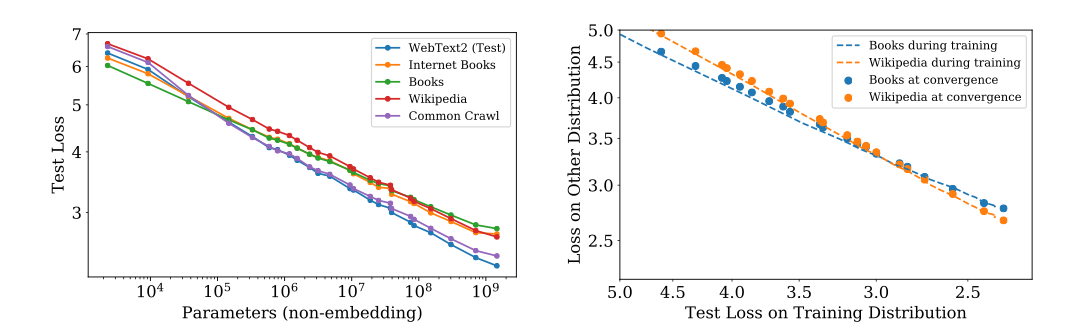
Open AI在2020年的大模型Scaling Law论文中发现,若将模型迁移到新的数据集,新数据集上的测试loss与训练数据集上的测试loss存在一个相对恒定的offset。随着模型规模的增大,训练数据集和新数据集上的测试loss近似同步下降。这也就意味着可以通过持续增大模型大小来降低模型在所有数据集上的loss。
这种优秀的泛化性给出了一种全新的探索方向:相比探索更复杂的模型结构,探索更大的模型是否能够成为深度学习的全新路径。
大模型的可预测性¶
传统深度学习的黑盒炼丹是被广为诟病的问题。虽然不乏丹术已至臻境的顶级丹师,但业务方和资本方是万万不敢在单次训练超一个月,耗资超百万的LLM训练交给这些丹师来负责的。如何预测一次训练能达到的精度,以及如何分配这种超百万级别的训练成本投入,就变成了训练LLM的必要条件。这方面比较重要的工作有两篇:一篇是OpenAI提出的Kaplan Scaling Law2,主要研究了模型loss和几个主要参数:模型参数规模N、训练数据规模D以及算力投入C之间的关系;另一篇是DeepMind提出的Chinchilla Optimal3,主要研究计算资源限定下,算力的分配问题,比如每个参数对应多少token。
Kaplan Scaling Law¶
Kaplan Scaling Law发表于2020年,同年OpenAI也正式发表了GPT3。因此从某种程度上来说,Kaplan Scaling Law即是对GPT3模型训练的一个总结,也是OpenAI坚定投入大模型和大算力的信心所在。先简单看下Kaplan Scaling Law的几个主要结论:
- 限定模型参数规模N,给足够大的数据集训练到收敛:
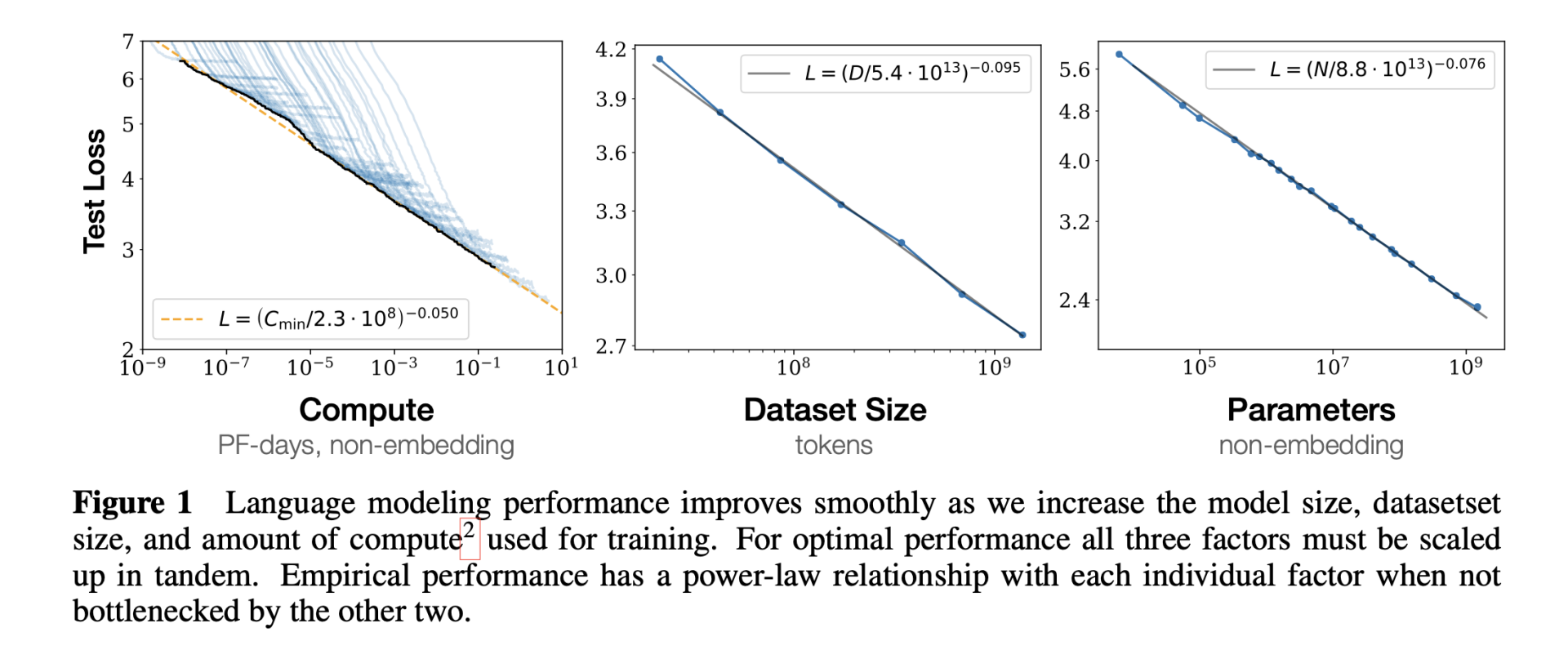
\(L(N) = \left (\frac{N_c}{N}\right ) ^{\alpha_N}; \alpha_N \simeq 0.076, N_c \simeq 8.8 \times 10^{13}\) - 限定数据规模D,通过early stopping 训练大模型:
\(L(D) = \left ( \frac{D_c}{D} \right)^{\alpha_D};\alpha_D \simeq 0.095, D_c \simeq 5.4 \times 10^{13}\) - 限定计算资源,给足够大的数据集、最优模型规模与足够小的batch size:
\(L(C_{min})=\left ( \frac{C_c^{min}}{C}\right )^{\alpha_C^{min}}; \alpha_C^{min} \simeq 0.050, C_C^{min} \simeq 3.1 \times 10^8\ (PFdays)\)
直观一点就是说影响loss的主要因素是N、D和C。随着三者的指数增长,loss线性下降:
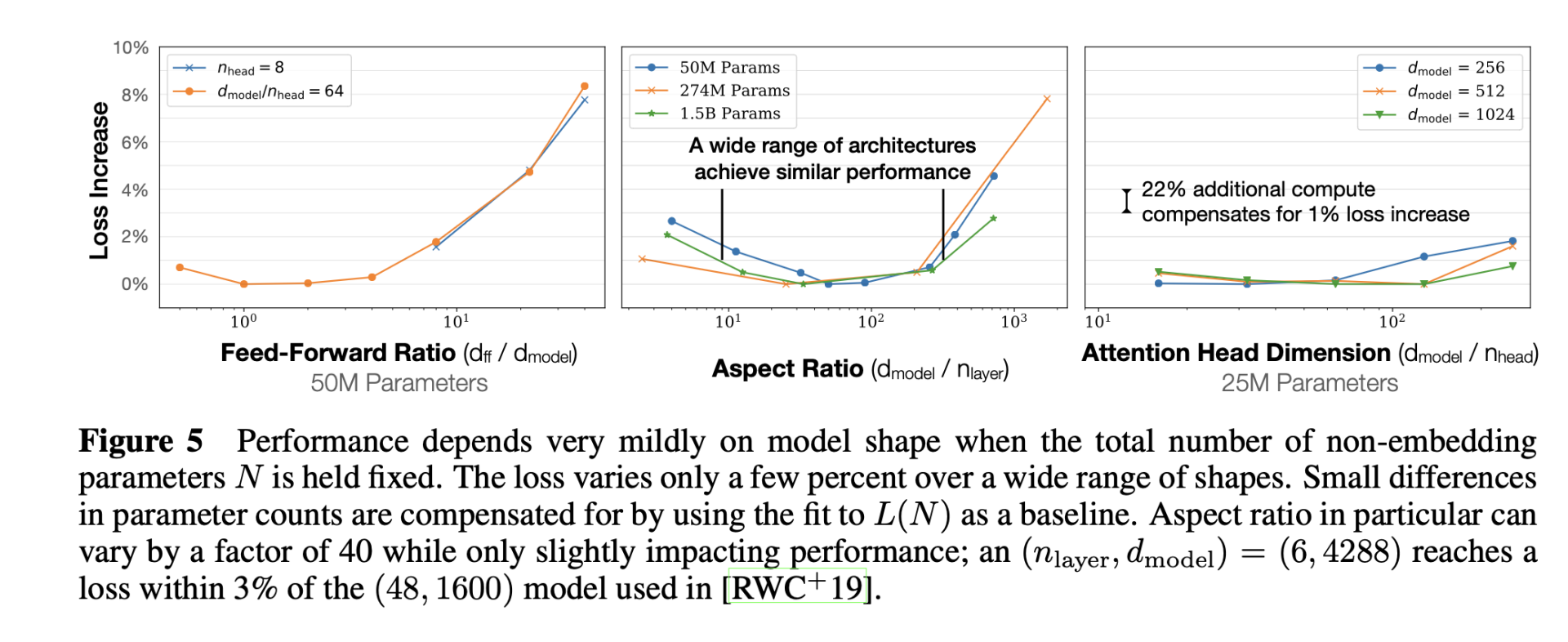
另一方面模型结构超参、学习器的超参没那么重要,整体对loss影响不大:
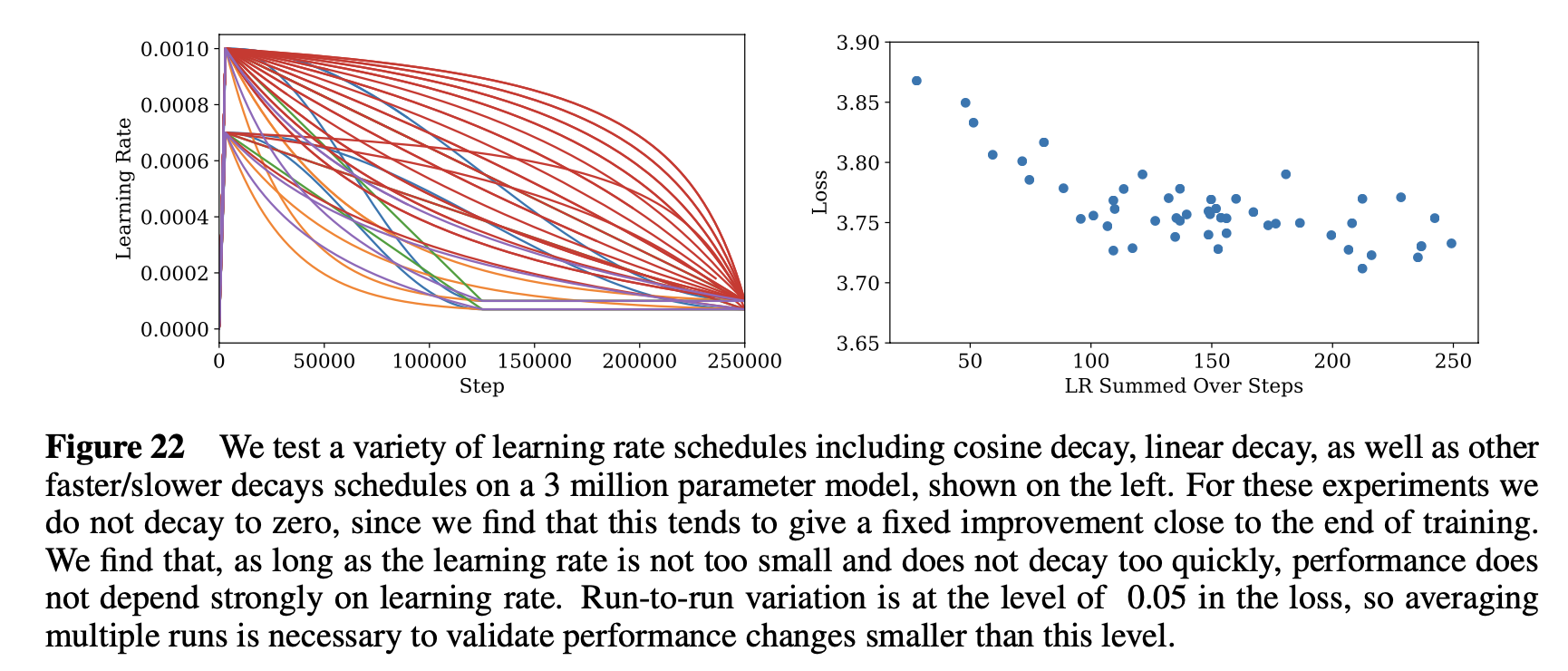
有些参数在一到两个尺度内变化,而对最终的loss影响在2%以内。而学习率只要不过于小,或者衰减过于迅速,对最终loss的影响并不大。
Kaplan Scaling Law最为重大的意义在于两点:
- 给出了影响模型效果的主要因素模型参数规模N和训练数据规模D,并认为其他超参是次要因素,影响不大,因此也就避免了LLM上继续黑盒炼丹;
- 给出了对Loss的预测方法,只要指数增长N、D和算力C,即可获得loss的线性改进;
根据Kaplan Scaling Law,GPT3的175B参数需要300B token训练,约每个参数1.7个token(具体参考kaplan vs chinchilla)。
Chinchila Scaling Law¶
Chinchila Scaling Law由DeepMind发表于2022年,同年Google发表了PaLM(Language Modeling with Pathways4)。Chinchila Scaling Law 关注求解算力约束下,最优模型规模N与数据规模D,即:
\(N_{opt}(C), D_{opt}(C) = \underset{N, D, \ s.t.\ FLOPs(N,D)=C}{\arg\min} L(N, D)\)
最终可以拟合出来N、D与算力C之间的关系:\(N_{opt} \propto C^a, D_{opt} \propto C^b\)。DeepMind给出了三种实现:
| 实现 | 参数\(a\) | 参数\(b\) |
|---|---|---|
| 固定N,搜索最优D | 0.50 | 0.50 |
| 固定C,搜索最优N和D | 0.49 | 0.51 |
| 拟合L(N,D),搜索最优N和D | 0.46 | 0.54 |
| Kaplan Scaling Law | 0.73 | 0.27 |
其中第三种实现拟合了如下关系
\(L(N,D)=E+\frac{A}{N^{\alpha}}+\frac{B}{D^{\beta}}\)
其中\(E\)刻画的是理想模型的loss,\(\frac{A}{N^{\alpha}}\)刻画的是有限模型参数对loss的影响,\(\frac{B}{D^{\beta}}\)刻画的是有限数据量对loss的影响。基于这个拟合出来的loss,可以绘制如下图像:
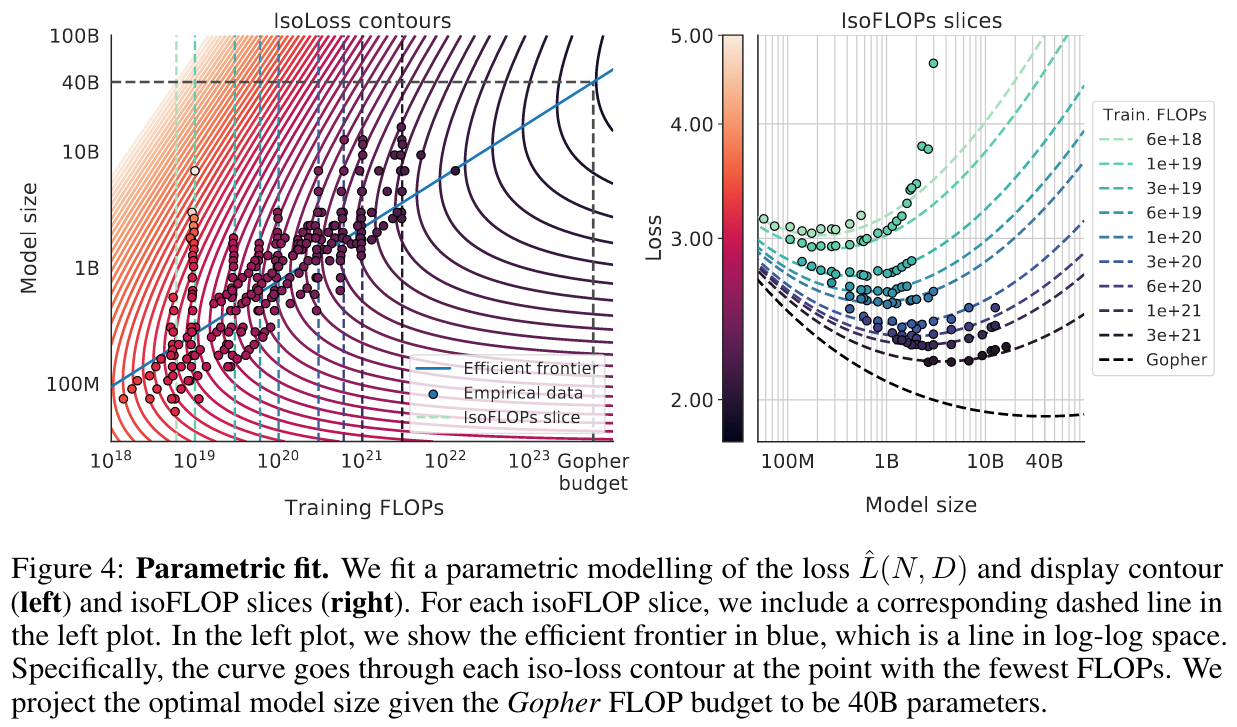
在左图中,每条loss等高线都有一个算力最优点,这些算力最优点又在log-log坐标上连成了一条近似直线,直线上的点即Chinchilla Optimal点。达到Chinchilla Optimal,每个参数大约需要20个token。
Beyond Power Law Scaling¶
Kaplan Scaling Law与Chinchilla Scaling Law所给出的都是数据与loss之间的Power Law,即数据指数增长,loss线性改进。根据Chinchilla Scaling Law,大模型的参数规模与数据量仍有2-3个数量级的提升空间:
| Model size(params) | Training tokens (round) | Training data used (estimate) | How much data is that? If 1 book is about 500KB of text (estimate) |
|---|---|---|---|
| 70B | 1.4 Trillion | 2.3TB | More books than in The Kindle store on Amazon US (6.4M). |
| 250B | 5 Trillion | 8.3TB | All 30 libraries at Yale University (16.6M). |
| 500B | 10 Trillion | 16.6TB | The Google Books collection (33.2M). |
| 1T | 20 Trillion | 33.3TB | The US Library of Congress (66.6M). |
| 10T | 200 Trillion | 333TB | All US public libraries combined (666M). |
| 100T | 2 Quadrillion | 3.3PB | All bibles ever sold worldwide (6.6B). |
| 250T | 5 Quadrillion | 8.3PB | A stack all the way to the Moon (16.6B). |
| 500T | 10 Quadrillion | 16.6PB | 4 books about every living human (33.2B). |
| Dataset sizes needed to align with Chinchilla data optimization for models5. |