Probing分布式探针系统的原型探索（二）：探针机制
引言
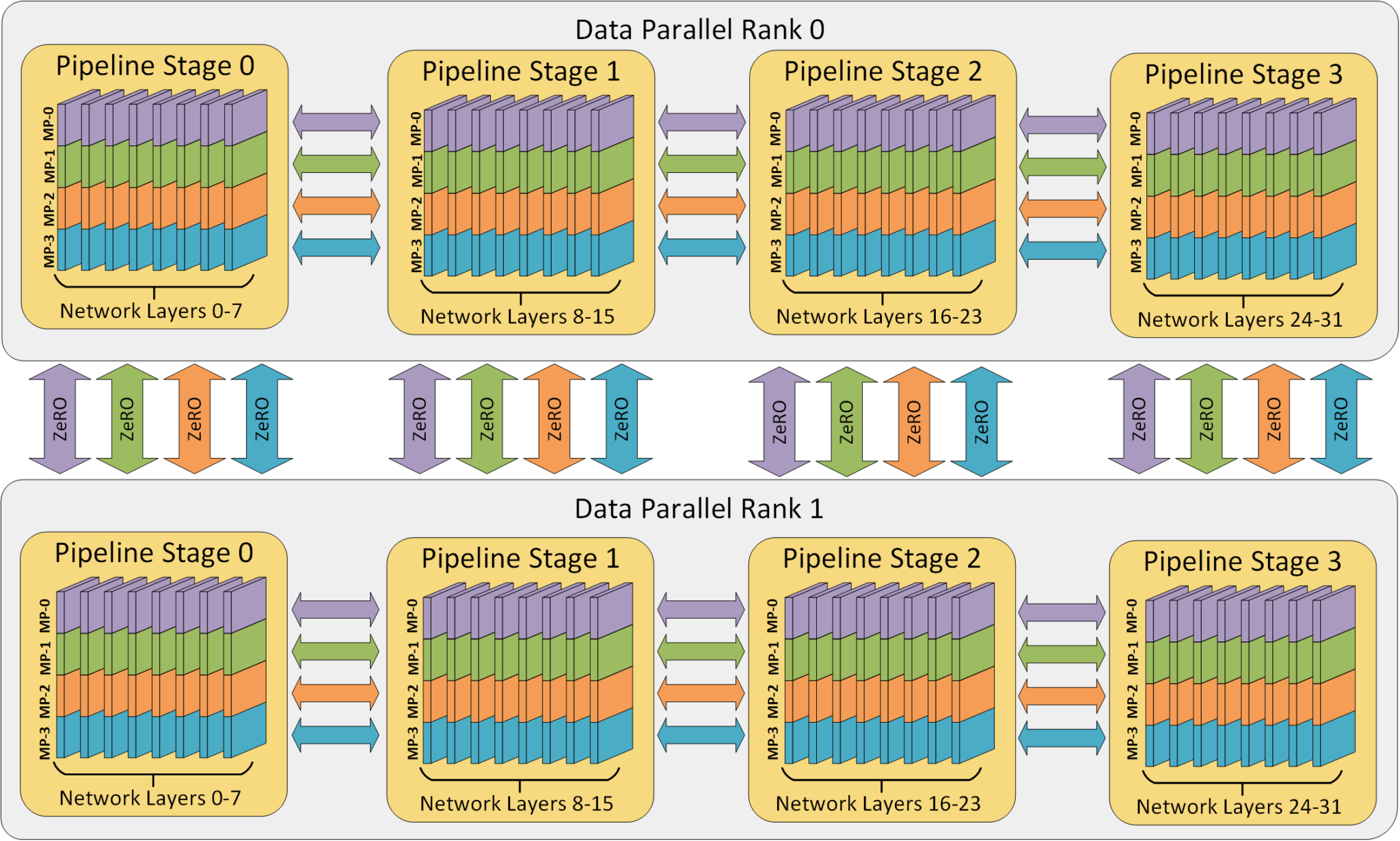
在前一篇文章中，我们介绍了探针思路的设计理念，以及 Probing 分布式探针系统的整体架构。本文将详细介绍 Probing 的探针机制，包括探针的动态注入与运行时加载，以及如何规避 C/C++常见的 ABI 兼容性问题。
为何探针的动态注入能力尤为重要？因为故障和性能问题的发生总是不期而至，我们无法保证每次出现问题时都能提前部署探针。因此，任何需要提前部署的工具都迫使工程师必须”复现”问题才能进行分析，这无疑大大增加了诊断难度和时间成本。而分布式场景下，复现的成本与难度更是倍增，毕竟难以预留千卡或者万卡资源来复现问题。
异构计算则是另一个让复现问题变得更加困难的因素。在异构计算中，程序状态不再单纯地保存在 CPU 的内存中，而是同时分布在 GPU、TPU 等计算单元的内存中。这些计算设备的内存中不存在类似调用栈这种结构化数据，我们无法简单地通过 dump 调用栈来捕获故障时刻的状态，而是需要 dump 整个计算设备的内存内容。对于常见的单机八卡配置，完整 dump 一次设备内存需要占用 640GB 的存储空间，这无疑是一个巨大的挑战。而管理这些数据的元数据通常存储在 Python 解释器中，这意味着必须开发一个跨设备、跨语言的调试工具，才能实现完整的故障诊断。
探针则是尝试另一种解决问题的思路：
- 通过动态注入，即可实现在任意条件下调试与诊断；
- 借助探针动态操作目标进程的 Python 解释器，利用其自然可以实现跨语言、跨设备的调试能力；
探针机制
探针注入的关键在于在目标进程的代码逻辑之外，额外向进程植入一段代码。常见的代码植入方式有两种：
LD_PRELOAD方法：通过LD_PRELOAD环境变量，可以让 ld.so 在加载目标进程的时候，优先加载指定的动态链接库从而实现代码植入。这种方法的优点是简单易用，但是只能在进程启动时生效，无法在进程运行时动态注入；ptrace方法：通过ptrace系统调用，可以在进程运行时动态修改进程的内存，从而实现代码植入。这种方法的优点是可以在进程运行时动态注入，但是需要对目标进程有一定的权限，且对目标进程的性能影响较大。
本文重点介绍ptrace方法的实现，LD_PRELOAD方法介绍的文章很多，本文不再赘述。
ptrace系统调用介绍
ptrace是一个 Linux 系统调用，用于监控和控制另一个进程。ptrace的调用方式如下：
ptrace 提供了一种控制目标进程执行的方法，它可以让调试器与目标进程进行交互，从而实现调试功能。__ptrace_request 常用的取值如下：
PTRACE_ATTACH: 附加到目标进程，使其成为当前进程的 tracee；PTRACE_INTERRUPT: 暂停目标 tracee；PTRACE_CONT: 让目标进程继续执行；PTRACE_DETACH: 释放目标 tracee；PTRACE_GETREGS/PTRACE_SETREGS: 读写目标进程寄存器；PTRACE_PEEKDATA/PTRACE_POKEDATA： 读写目标进程内存，一次一个 WORD；/proc/<pid>/mem: 大块读写内存；
常见的一个 debugger 的工作流程如下：
- attach 到目标进程；
- 通过读写目标进程 TEXT 段插入断点；
- 恢复目标进程执行，并用
waitpid等待目标进程断点暂停； - 等到目标进程暂停，通过读写内存查看信息；
探针注入流程
这里参考了 https://github.com/Artemis21/ptrace-inject 项目，进行了一些修改。注入流程如下：
- 通过
PTRACE_ATTACH附加到目标进程；
Rust 中可以通过pete库对ptrace的封装来使用ptrace系统调用：
let mut tracer = pete::Ptracer::new();
tracer
.attach((&proc).into())
.context("failed to attach to given process")?;
log::trace!("Attached to process with PID {}", proc);
- 写入 shellcode 到目标进程的内存中；
首先找到一处合适的内存地址，具有执行权限，可以写入 shellcode。这里我们通过读取目标进程的内存映射信息，找到一个具有执行权限的内存区域：
/// Find a suitable address to inject the shellcode into.
pub(crate) fn find_executable_space(&self) -> Result<u64> {
log::trace!("Finding executable space in target process");
self.0
.maps() // 读取 /proc/<pid>/maps 文件，获取进程的内存映射信息
.context("failed to read process memory maps to find executable region")?
.into_iter()
.find(|m| m.perms.contains(process::MMPermissions::EXECUTE))
.map(|m| m.address.0)
.ok_or_else(|| {
anyhow::anyhow!("could not find an executable region in the target process")
})
}
上述代码通过读取/proc/<pid>/maps文件，获取进程的内存映射信息，找到一个具有执行权限的内存区域。接下来我们先保存这个内存区域的内容，然后写入 shellcode：
// 打开 /proc/<pid>/mem 文件，供后续读写内存使用
let mem = fs::OpenOptions::new().read(true).write(true)
.open("/proc/<pid>/mem")?;
// 根据偏移量，读取目标进程的内存
let len = mem.read_at(data, addr)?;
// 将shellcode写入目标进程的内存
let len = mem.write_at(shellcode, addr)?;
其中data是一个[u8; 1024]大小的数组，用于保存原内存区域的内容；shellcode是我们要写入的 shellcode，内容如下
/// The x64 shellcode that will be injected into the tracee.
const SHELLCODE: [u8; 6] = [
// Nop slide to make up for the fact that jumping is imprecise.
0x90, 0x90, // nop; nop
// The tracer does most of the work by putting the arguments into the
// relevant registers, and the function pointer into `r9`.
0x41, 0xff, 0xd1, // call r9
// Trap so that the tracer can set up the next call.
0xcc, // int3
];
shellcode 主要由三部分组成：
- 两个
nop指令，避免跳转时的不精确性带来问题； - 一个
call r9指令，调用r9寄存器中的函数指针，此处调用会遵循 X86_64 下的标准调用协议，通过寄存器传参； - 一个
int3指令，触发中断，控制流程回到 tracer；
- 通过设置寄存器调用目标函数：
在 tracer 中设置寄存器，让目标进程调用函数：
self.tracee
.set_registers(pete::Registers {
rip: shellcode_address,
// shellcode会通过r9寄存器调用函数
r9: fn_address,
// 根据x86-64 ABI要求，将函数入参传递到寄存器中
rdi,
rsi,
// 根据x86-64 ABI要求，确保栈指针对齐到16字节
rsp: self.saved_registers.rsp & !0xf,
..self.saved_registers
})
函数fn_address是我们要调用的函数在目标进程中的虚拟地址，rdi和rsi是根据 x86-64 调用约定传递的前两个函数参数，rsp是栈指针，必须对齐到 16 字节以符合 ABI 要求。特别注意，fn_address必须是目标进程地址空间中的有效地址，否则会触发SIGSEGV信号导致进程崩溃。而目标进程的地址是不固定的，我们需要通过函数相对 so 文件的偏移量来计算。首先分别获取libc.so在 tracer 和 tracee 中的地址，可以通过/proc/<pid>/maps文件获取每个 so 映射到内存的地址。再根据函数在 tracer 中的地址计算函数在libc.so中的偏移量。最后在 tracee 中根据libc.so的地址与函数偏移量计算目标函数在 tracee 中的真实地址，即可根据该地址进行调用。
获取函数真实地址的代码比较冗长，感兴趣的话可以参考仓库中的源码。
通过上述步骤，我们可以在 tracee 中调用dlopen函数，加载动态链接库，实现动态注入。
探针实现
ptrace只是帮助我们实现了探针的动态注入，而真正的探针逻辑还需要我们自己实现。根据前文所述，借助ptrace可以让目标进程调用dlopen来加载动态链接库。而在动态库加载的过程中，会读取 ELF（Executable and Linkable Format） 文件中的.init_array段，该段中存放了一系列初始化函数的地址。C/C++编译器一般支持__attribute__((constructor))属性，可以将函数注册到.init_array段中。
而 Rust 中可以通过#[ctor]宏实现类似的功能：
Probing 的注入框架不仅支持其内置探针模块，还支持用户自定义的探针库，提供了极高的扩展性。关于探针的具体设计细节，我们将在后续文章中深入探讨。
ABI 兼容性
传统的 C/C++项目经常受 ABI（Application Binary Interface）兼容性的困扰。常见的 ABI 兼容性问题有两类：
- glibc 中函数的版本问题：为了保证 ABI 的兼容性，glibc 中的函数会有多个版本，比如
malloc函数就有malloc@GLIBC_2.2.5、malloc@GLIBC_2.3等多个版本。而动态链接库在链接时会在当前 glibc 中选取一个最新的版本，这就导致了在较新的系统下编译的 so 文件在较旧的系统上无法运行； - C++的 ABI 问题：C++的 ABI 问题主要由于最近几年 C++标准的更新较快，导致 libstdc++库的 ABI 不断变化。其中最为常见的一种错误是
std::string类型在 C++11 标准中引入了短字符串优化（SSO）机制，导致std::string的内存布局发生了变化。而在 C++11 之前编译的 so 文件在 C++11 标准下运行时，会出现内存布局不一致的问题；
Probing 主要通过两种方式解决 ABI 兼容性问题：纯静态链接与 zigbuild。
纯静态链接
静态链接是解决 ABI 兼容性的一种经典方法，通过将所有依赖库代码打包到一个 so 文件中，并在链接阶段完成所有符号的解析，从而避免了运行时出现 ABI 问题。Rust 在构建 so 文件的时候默认使用纯静态链接，能够很大程度上避免 C/C++项目中的 ABI 兼容性问题。
zigbuild
Zig 是一种新兴的系统级编程语言，内置完整的交叉编译工具链，可针对不同 glibc 版本生成二进制文件：
这使得使用 Zig 工具链构建的 so 文件可以通过指定低版本的 glibc 来增加 so 文件的兼容性。
cargo-zigbuild是 Rust 构建工具cargo的一个扩展，可以在编译时指定 glibc 的版本，并借助 Zig 的工具链完成 so 文件的链接。
打包发布
前文已经讨论了探针的动态注入与 ABI 兼容性问题，两者都尽最大的可能让 Probing 可以在任意环境下直接运行，而无须额外的配置。接下来我们将讨论 Probing 的打包发布问题，这是让 Probing 真正成为一个通用的工具的关键。
二进制工具发布通常有三种渠道：
- 发布源码：将源码发布到 github 等代码托管平台，用户可以自行编译；但往往构建一个复杂项目的环境是非常困难的，尤其是在分布式环境下；
- 发行版包管理器：将二进制工具打包成 rpm、deb 等包，发布到发行版的包管理器中，用户可以通过包管理器安装；但是不同发行版的包管理器不同，维护成本较高；并且同一个发行版的不同版本需要维护不同的包；
- pip/conda 等第三方发布平台：将二进制工具打包成 pip/conda 包，发布到第三方平台，用户可以通过 pip/conda 安装；但是这种方式往往需要用户安装额外的包管理器，不够方便；
不过对于 AI 领域的工具来说，Python 是必不可免的，因此基于 Python 包管理工具 pip 或者 conda 来发布 Probing 是一个不错的选择。
不同于一般的 python 包，Probing 是一个以 Rust 为主要开发语言的工具，因此并不适合使用 setup.py 等传统方式来构建 python 包。这里我们选择直接使用脚本来打包whl:
def write_wheel_file(filename, contents):
with WheelFile(filename, "w") as wheel:
for member_info, member_source in contents.items():
...
return filename
def write_wheel(out_dir, *, name, version, tag, metadata, description, contents):
name_snake = name.replace("-", "_")
wheel_name = f"{name_snake}-{version}-{tag}.whl"
dist_info = f"{name_snake}-{version}.dist-info"
return write_wheel_file(
os.path.join(out_dir, wheel_name),
{
**contents,
f"{dist_info}/METADATA": make_message(...),
f"{dist_info}/WHEEL": make_message(...),
},
)
def write_probing_wheel(
out_dir, *, platform="manylinux_2_12_x86_64.manylinux2010_x86_64"
):
...
for name, path in {
"probing": "target/x86_64-unknown-linux-gnu/release/probing",
"libprobing.so": "target/x86_64-unknown-linux-gnu/release/libprobing.so",
}.items():
zip_info = ZipInfo(f"probing-{metadata["version"]}.data/scripts/{name}")
zip_info.external_attr = (stat.S_IFREG | 0o755) << 16
with open(path, "rb") as f:
contents[zip_info] = f.read()
...
return write_wheel(
out_dir,
name="probing",
version=metadata["version"],
tag=f"py3-none-{platform}",
metadata={...},
description=description,
contents=contents,
)
def main():
wheel_path = write_probing_wheel("dist/")
with open(wheel_path, "rb") as wheel:
print(f" {wheel_path}")
print(f" {hashlib.sha256(wheel.read()).hexdigest()}")
if __name__ == "__main__":
main()
该脚本主要使用wheel包中的WheelFile类来构建whl文件，并将构建出来的二进制写入到probing-{version}.data/scripts目录下。此外需要提供METADATA和WHEEL文件，分别用于描述包的元信息和 wheel 的版本信息。
总结
本文主要讨论了 Probing 的核心机制——探针注入，并讨论了如何将这一机制变成一个通用工具，让其能使用到复杂多样的生产环境中，能够快速发布给尽可能多的用户。所有这些设计都是为了 Probing 的一个核心设计理念：解决问题时，应直接面对根本问题，避免陷入工具配置、环境搭建等元问题的循环中。或者可以认为这一设计理念是马斯克第一性原则的一种体现，缩短解决问题的路径，提高解决问题的效率。
在下一篇文章中将会介绍探针 so 的设计与实现。
